
After receiving positive feedback on the article giving an insight into how astrodynamics simulations are done, I have decided to start a small series of articles in which I will try to give you some basic pointers on how to get started making astrodynamics simulations. Author: Ondřej Hladík
Astrodynamics is one of those things that are easy to learn but hard to master, especially once you start getting into three- and n-body problems, but this should not dissuade anyone from trying to learn this very interesting and captivating craft.
First, we need to introduce our software. We will be using GMAT, an open-source mission analysis software created by NASA and other partners. Once you install and open it, you should see the following interface: 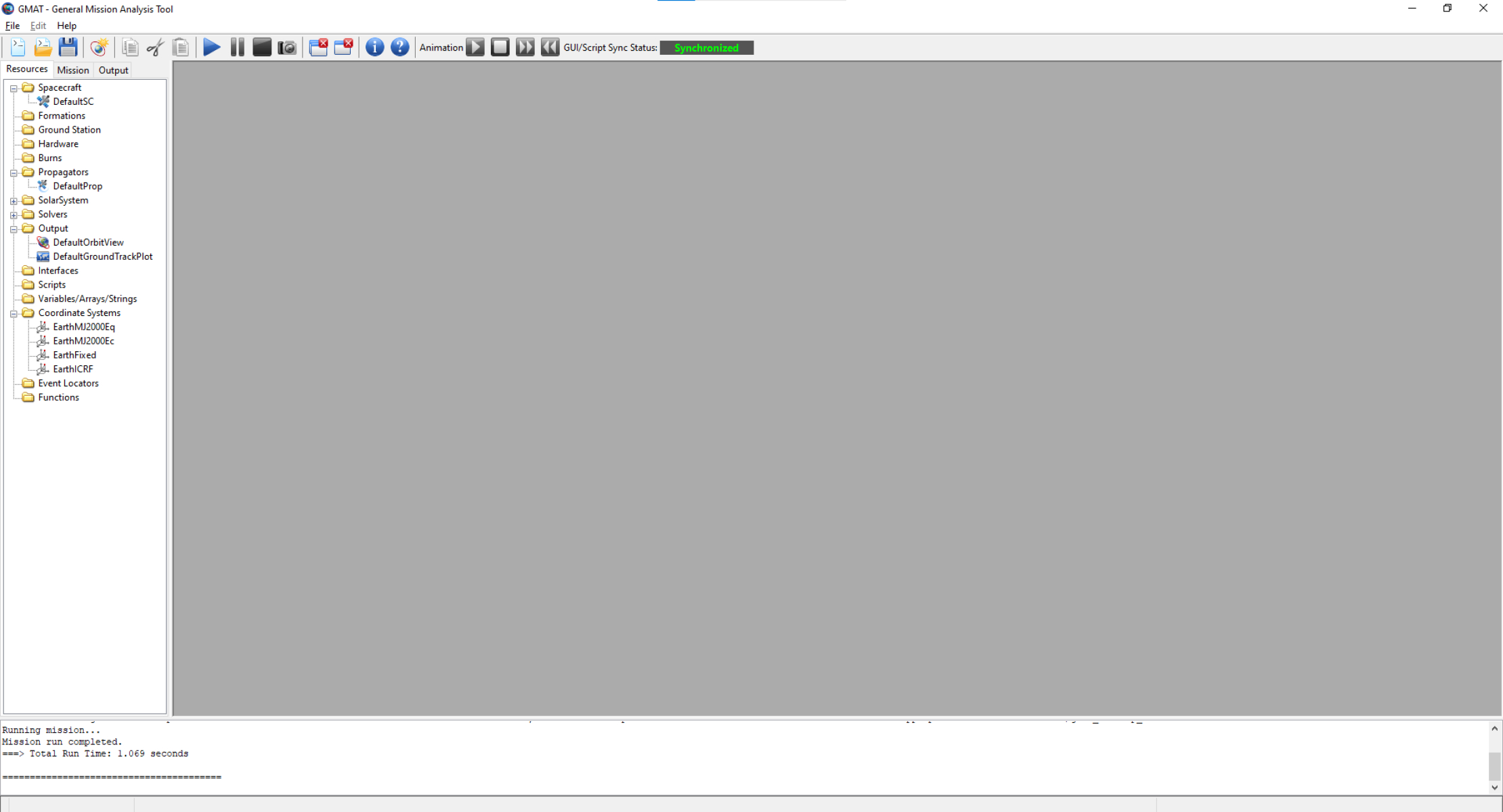 In the top left, you can see three tabs: Resources, Mission, and Output. The Resources tab includes your spacecraft, ground stations, hardware, and so on, that you use in your simulations as well as all the outputs defined within it.
In the top left, you can see three tabs: Resources, Mission, and Output. The Resources tab includes your spacecraft, ground stations, hardware, and so on, that you use in your simulations as well as all the outputs defined within it.

For the first simulation, we will be only working with our spacecraft. You can open its properties by double-clicking it. You can see that there are many different tabs you can open. All of these have their purpose and we will get to them in later tutorials. For now, we will focus on setting up our epoch and starting orbit.
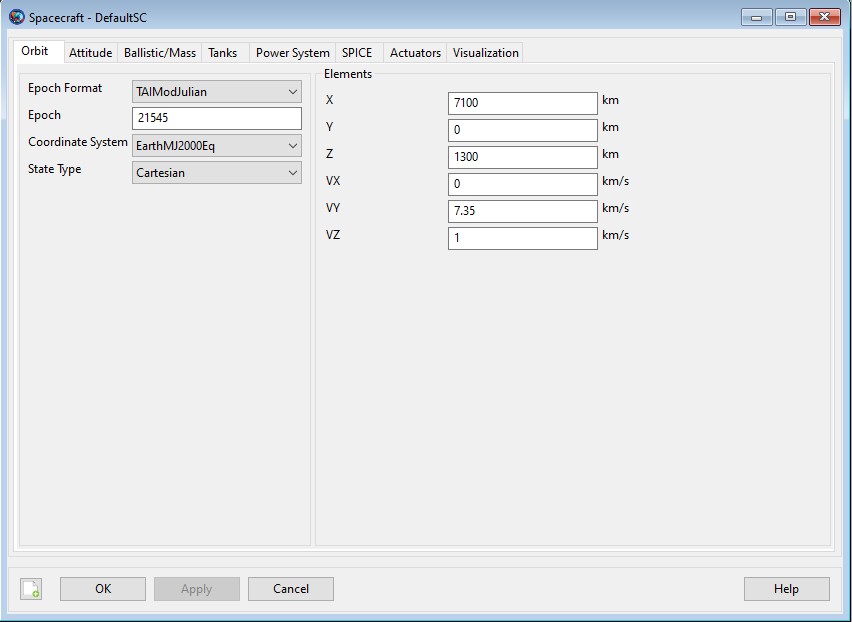 Let’s start with the epoch. While the list of options might seem long at first, it effectively boils down to two choices. First you are choosing between Modified Julian Day and Gregorian date. The first option is simply count of days since noon of 5th January 1941 while Gregorian date is simply the date you would find in your calendar or in the lower right-hand corner of your screen if you are using Windows. The other decision is much more of minutiae, there are five options for the definition of the time. A1 refers to USNO atomic time scale, TAI to International Atomic Time, UTC to Universal Coordinated Time, TDB for Barycentric Dynamic Time, and TT for Terrestrial Time. Try switching between them and you will see that they are very similar.
Let’s start with the epoch. While the list of options might seem long at first, it effectively boils down to two choices. First you are choosing between Modified Julian Day and Gregorian date. The first option is simply count of days since noon of 5th January 1941 while Gregorian date is simply the date you would find in your calendar or in the lower right-hand corner of your screen if you are using Windows. The other decision is much more of minutiae, there are five options for the definition of the time. A1 refers to USNO atomic time scale, TAI to International Atomic Time, UTC to Universal Coordinated Time, TDB for Barycentric Dynamic Time, and TT for Terrestrial Time. Try switching between them and you will see that they are very similar.
For now, we will skip over the Coordinate System, which is a very interesting and useful topic, that will hopefully be explored in one of the later installments, and we will go to State Type. This dictates what 6 values about your spacecraft you will need to provide that will dictate its orbit. Right now, Cartesian should be selected and you can see that you would be entering coordinates and velocities. While useful for a whole plethora of things, those of you who are more familiar with astrodynamics may feel more comfortable with Keplerian elements and those coming from the field of astronomy may be more inclined to use the spherical coordinate system. There are no wrong answers here, but for purposes of this tutorial we will be using “Modified Keplerian” as it is one of the easier ones to imagine in practice. After selecting that, your elements should look something like this:
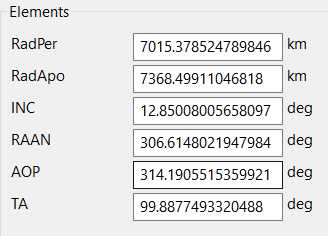
The first line labeled “RadPer” radius at periapsis, the closest your spacecraft is to the central body it is orbiting. The second line “RadApo” is its polar opposite, the radius at the most distant point from your central body, the apoapsis. The third line is the spacecraft’s inclination. This angle can range from 0 to 180. The net line is Right Ascension of the Ascending Node, which is quite a mouthful and it is one of the harder-to-imagine orbital elements. Imagine Earth’s equatorial plane. Then imagine that on this plane there is a line towards a reference point, in the case of orbits around Earth it is the First Point of Aries, and another line towards where the point at which the spacecraft crosses the equatorial plane in the upward direction, traveling north. Compared to that the two remaining lines are simple. AOP stands for the argument of periapsis and this is the angle between the X-axis and a line that connects your spacecraft’s periapsis to the center of the Earth. Lastly, TA stands for True Anomaly, which dictates your spacecraft’s current position similarly to AOP, only the two lines from the center of Earth go through your periapsis and your current position. Try to tweak around these numbers and observe their effects, you can run the simulation either by pressing the blue play button or by pressing F5.
Now that we have gone through the important but somewhat dull introductory part of this article, let’s get to the part why most of you are reading this, the simulation. We will start easy with a very simple mission to raise perigee.
Let’s set up the spacecraft for our simulation. When setting up the initial orbit try to start with values other than the radius of periapsis and apoapsis at zero and observe how each value changes the orbit. We will be using the following orbit: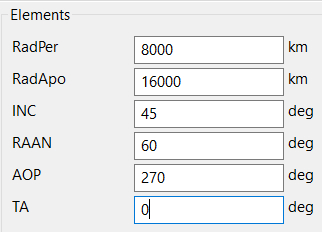
Before we start working on the simulation itself, we need to discuss what we want to do. Spacecraft maneuvers are not always very intuitive at first. Rather than a movement and maneuvers think about it in terms of energy, since, in the absence of a thick atmosphere, what decides your trajectory is momentum and exchange of energy between kinetic and potential energy. This means that when we want to raise periapsis or apoapsis, we always perform the maneuver at the opposite point of the orbit. So, in our case, we need to get our spacecraft to the apoapsis and perform the maneuver there.
Now you will need to switch your tab from Resources to Mission and we can start setting up the simulation. You will notice that there already is one command present, propagate. This is a basic command that propagates the satellite forward in time until the end condition is met. By double-clicking on it you will open a window in which you can inspect the command and change its properties. Right now, the stopping condition is “ElapsedSecs” which is just the number of seconds it moves forward in time. By clicking the three dots on the left of the parameter column it will open a dialog window in which you can select a new stopping condition. So go ahead and choose Apoapsis as your stopping condition.
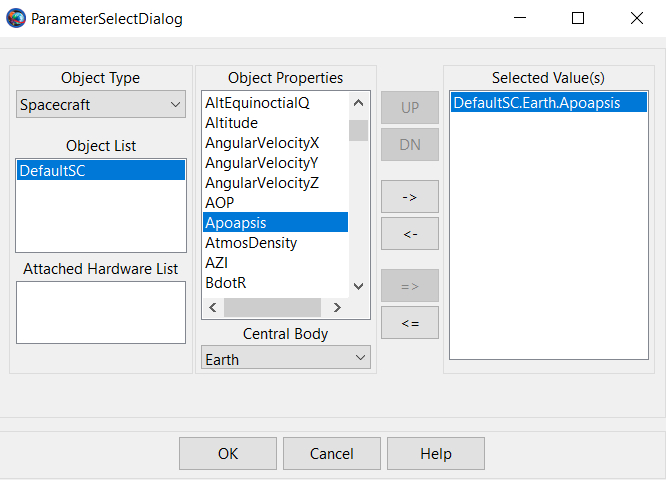
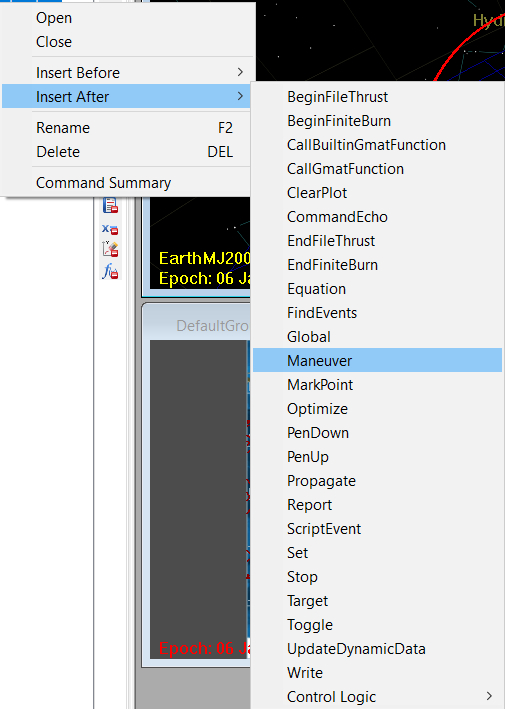
 Now just click OK or Apply and the first step in setting up the simulation is complete. Next, we will need to add our maneuver. This will be achieved by right-clicking on the Propagate command and adding a Maneuver command. Just like in the picture.
Now just click OK or Apply and the first step in setting up the simulation is complete. Next, we will need to add our maneuver. This will be achieved by right-clicking on the Propagate command and adding a Maneuver command. Just like in the picture.
Once that is added we will need to take one more detour to the Resources tab. You will notice that a new item, “DefaultB”, has been added. This is the default impulse maneuver. Like with other ones, double-clicking it will bring up the menu in which you can adjust it. You will see the coordinate system, and take specific note of the axes. VNB means velocity, normal, and binormal, meaning that Element1 is always pointing in the direction of the spacecraft’s movement. In the following section, we are setting up the delta-v vector and magnitude. Since we want to simply raise the periapsis, we need to increase our velocity at apoapsis, so we insert our chosen value into the first box and click the OK button.

Finally, switch back to the Mission tab and add one more propagate. Here I would recommend selecting the stopping condition of elapsed days and setting it to some low single-digit value, for example 5. This way your satellite will certainly perform multiple full orbits. The finished mission should look something like this
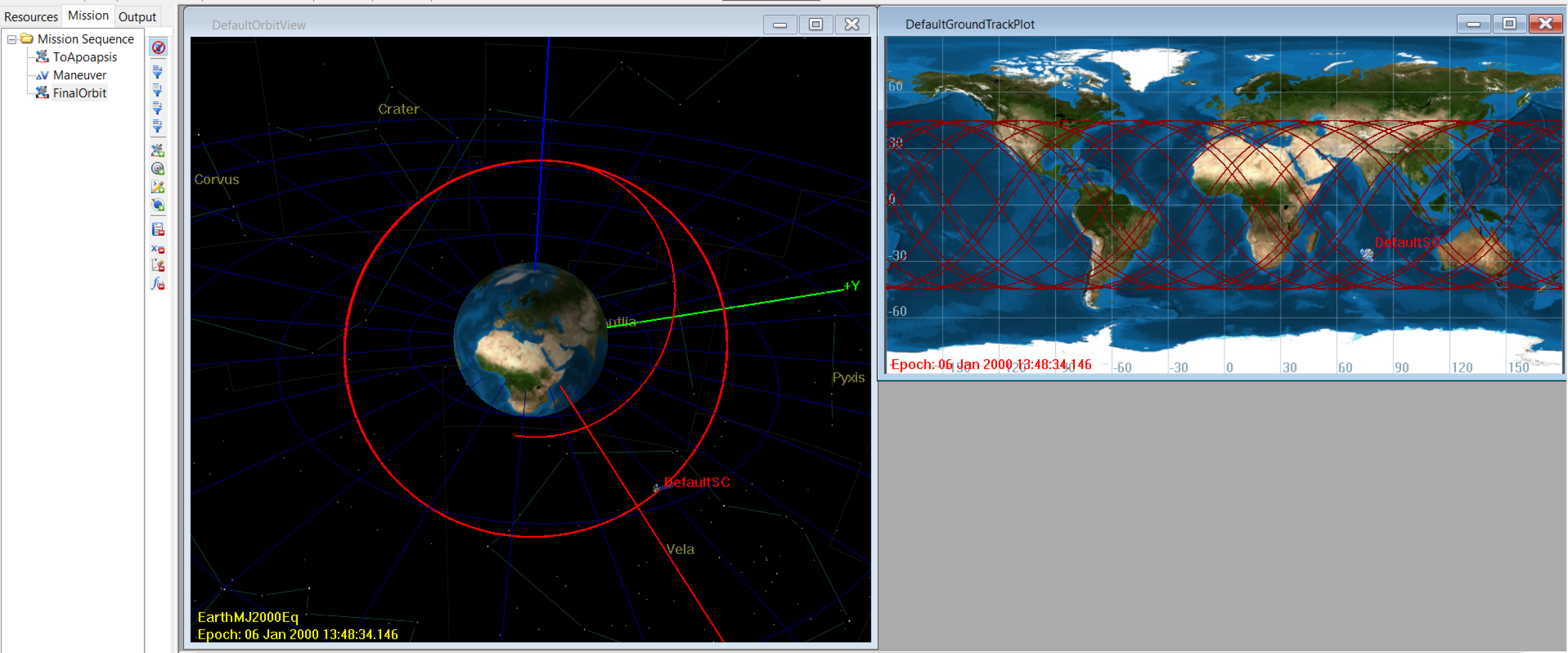 If you have gotten all the way here, I would like to thank you for spending some time with my article and I sincerely hope that it helped you take your first steps in simulations of astrodynamics.
If you have gotten all the way here, I would like to thank you for spending some time with my article and I sincerely hope that it helped you take your first steps in simulations of astrodynamics.